The X-Pol method, initially called the MODEL theory, is a general, and rigorously defined theory, which can be used either as an electronic structure method for macromolecular systems or as a quantum force field for biomolecular and materials simulations. Depending on the problem of interest or one's personal flavor, ab initio and semiempirical molecular orbital theory or density functional theory can be used uniformly or in a hybrid.
The X-Pol theory is based on a hierarchy of three approximations. They were first introduced in 1997, subsequently used for Monte Carlo and molecular dynamics simulations of liquid water, liquid hydrogen fluoride, and a fully solvated BPTI protein, and a summary of these principles was recently outlined in Lingchun Song, Jaebeom Han, Yen-lin Lin, Jiali Gao, Journal of Physical Chemistry A, 2009, 113, 11656.Each approximation allows a significant reduction of computational costs and the introduction of a set of parameters to be optimized to strive for accuracy.
The X-Pol potential for macromolecular systems is being developed collaboratively between the groups of Professor Gao and Professor Don Truhlar. The feasibility of the X-Pol potential for modeling biomolecular systems has been recently demonstrated.
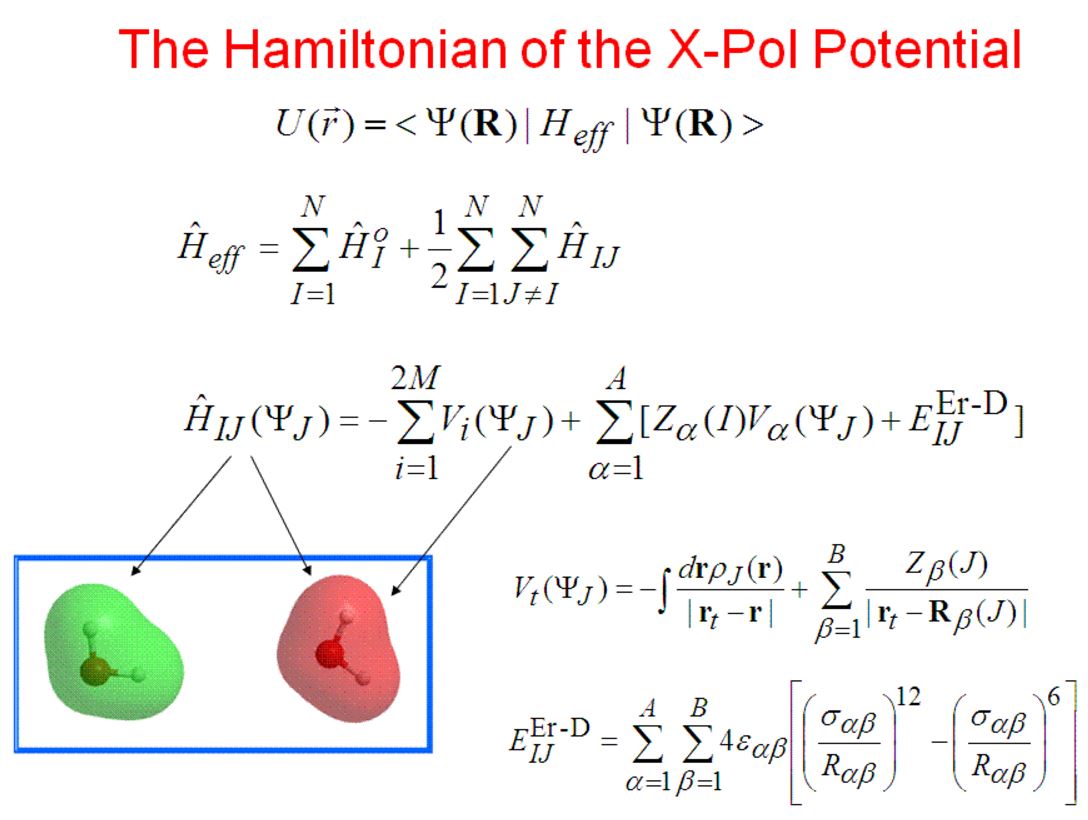
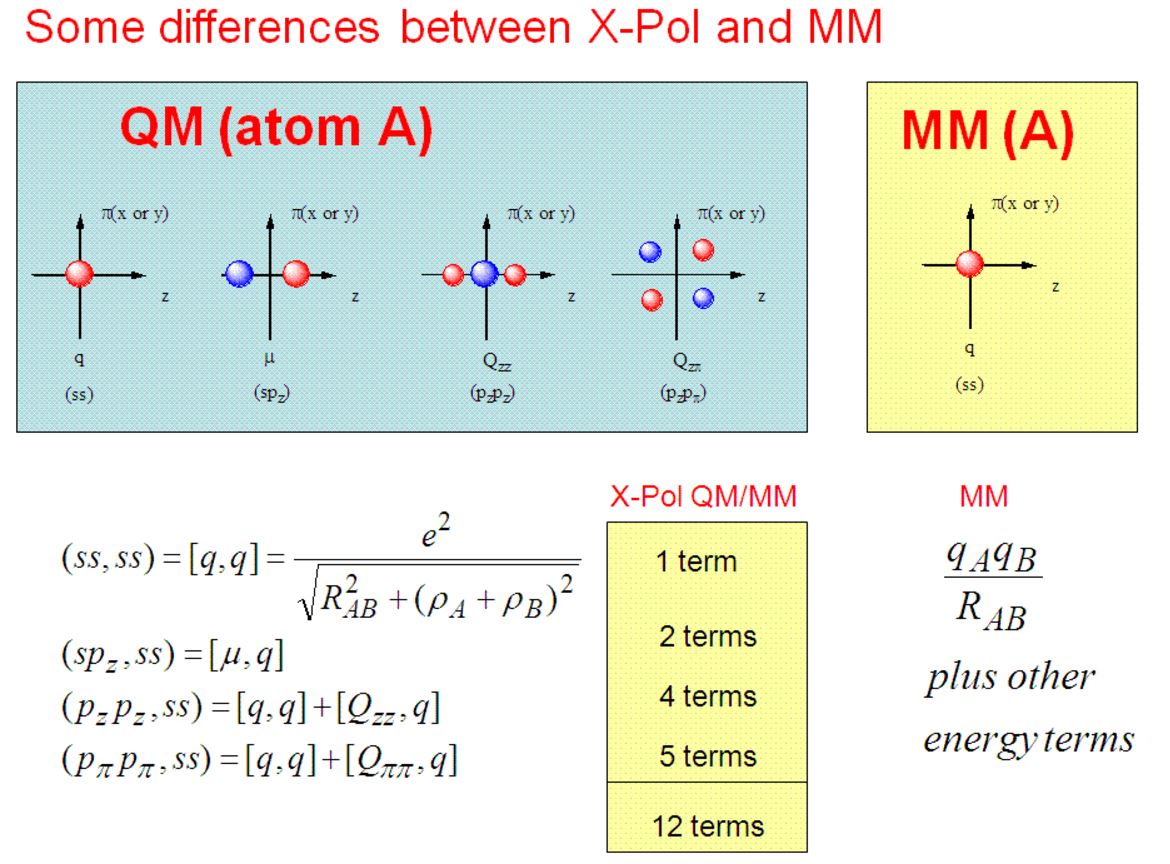
Relevant Paper: The Generalized X-Pol Theory and Charge Delocalization States
Comparison of X-Pol and Fragment Molecular Orbital Method
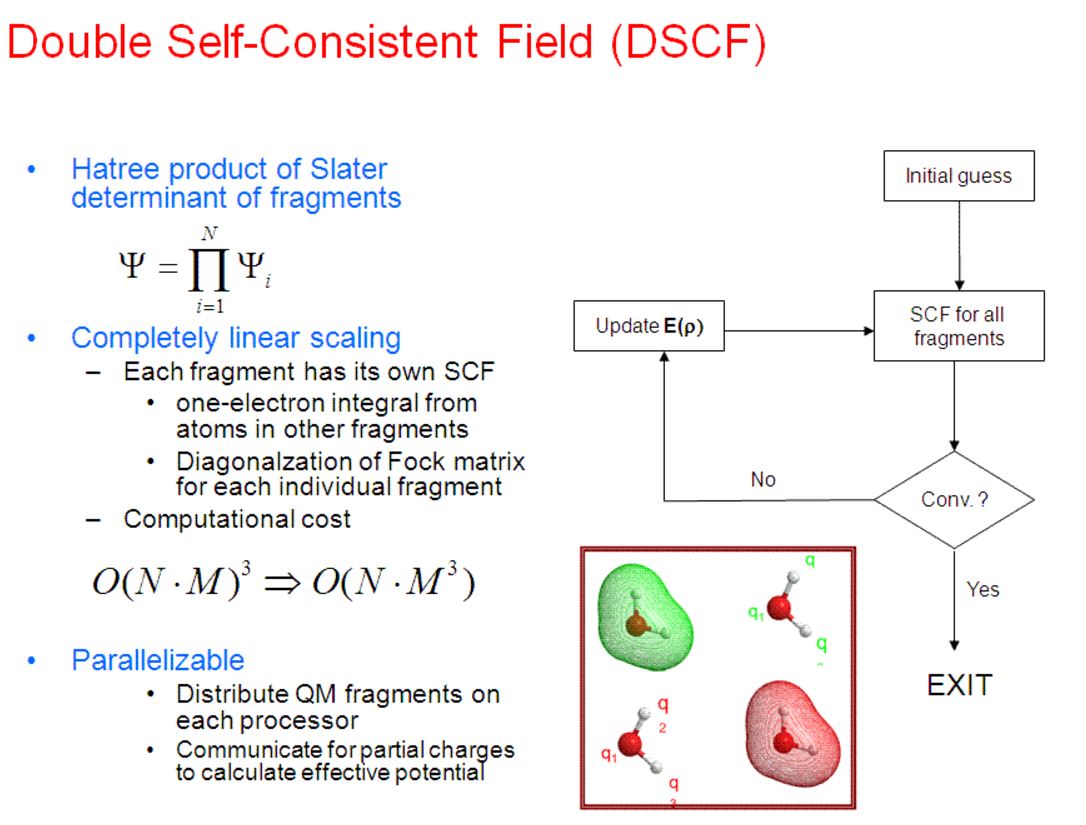
There is little, if any, difference in the double SCF (DSCF) procedure between the initial DSCF version of the X-Pol method (called MODEL), first introduced in January, 1997 (J. Phys. Chem. B 1997, 101, 657), and fragment molecular orbital, appeared more than two years later in 1999 (Chem. Phys. Lett. 1999, 312, 319; and 313, 701). There is a slight difference in energy computation; the X-Pol energy is obtained directly as the expectation value from the SCF wave function, whereas an energy addition-subtraction scheme is used with an additional dimer term, accounting mainly for the exchange repulsion energy between different fragment blocks. In view of the appealing features of the block localization of a macromolecular system to be computationally efficient, and in view of the fact that the exchange repulsion is short-ranged, and in view of the experience that charge transfer and dispersion interactions can be empirically modeled, the X-Pol theory treats the interfragment charge transfer and exchange repulsion by effective external potentials and by Lennard-Jone terms, respectively.
The original DSCF procedure is self-consistent both for each individual subsystem (fragment) polarized by the full electrostatic field of the rest of the system and for the total electronic energy of the entire system. However, this procedure does not yield the exact variational ground state energy. Although the difference between the DSCF energy and the variational ground state energy is minimal, analytical gradients cannot be obtained from the DSCF wave function. The DSCF procedure was derived in 1997 for the purpose of carrying out Monte Carlo simulations, which does not require interatomic forces, and the procedure is perfectly adequate. It is not so for efficient gemometry optimization and practical molecular dynamics simulations. A variational approach can easily be obtained in the X-Pol method, making it possible to determine analytical gradients.
The fragment molecular orbital (FMO) approach uses the DSCF method in SCF optimization.
Comparison of X-Pol and Divide & Conquer
There is similarity between the X-Pol method and Weitao Yang's Divide and Conquer scheme, which lies in dividing a full system into N subsytems such that a large diagonalization problem is reduced to diagonalization of N smaller sizes. However, it is necessary in D&C to use a large buffer region for each subsystem, typically 50 to 100 times the size of the subsystem, to obtain reasonable results. On the other hand, in the X-Pol method, there is no need for such a buffer region in diagonalizing the Fock matrix to construct the density matrix for the subsystem (fragment), and the Coulomb potential from the entire system is included. In contrast, long-range electrostatic (Coulomb) interactions are neglected beyond the buffer region (although a D&C plus X-Pol can easily be defined to circumvent this problem in typical D&C calculations reported so far (2009)). Thus, if all is equal, the X-Pol method is at least M**3 times more efficient (where M is the number of subsystems in the buffer region for each subsystem optimization) than the D&C scheme.
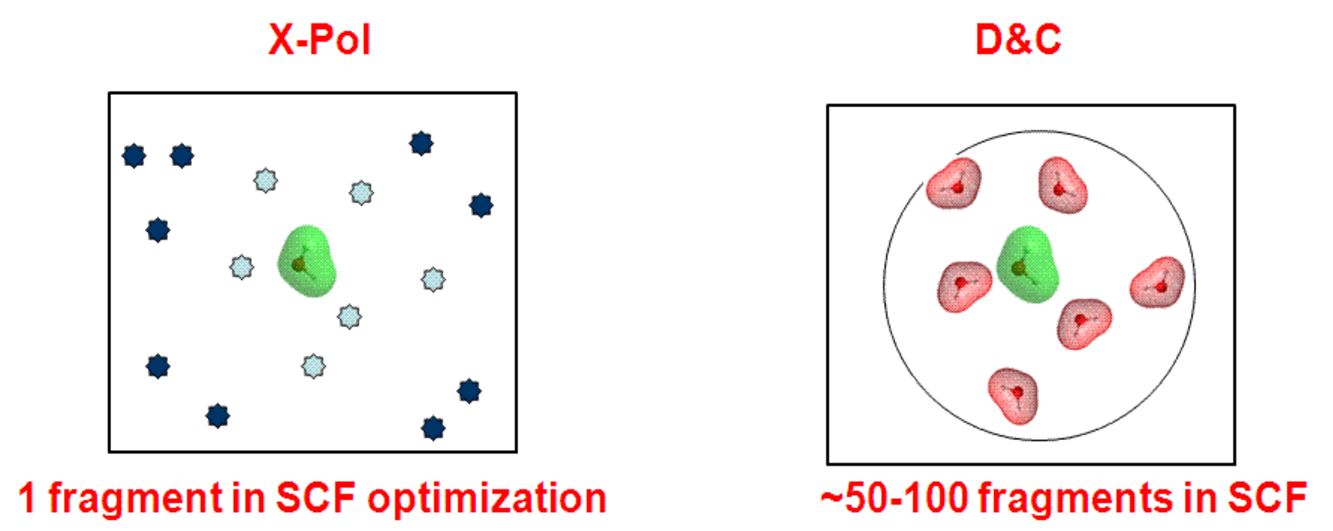
There are many major differences between the X-Pol and D&C methods:
